2.1.1 ベクトルとは何か
ベクトルとは、複数の数値を1つのまとまりとして扱うための数学的な道具です。最も直感的には、位置や移動を表す「矢印」として理解されることが多いです。
たとえば、2次元平面上の点 (3, 4) は、原点から右に3、上に4進んだ点を意味します。これは、ベクトルとして (3, 4) と表すことができます。3次元空間であれば (1, 0, -2) のように表されます。
一般に、n個の数の並び
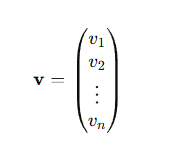
をn次元の列ベクトルと呼びます。
ベクトルの主な用途は以下の通りです:
- 幾何的な方向と長さの表現(物理や画像処理)
- データの特徴の表現(機械学習)
- 数学的操作の単位(線形変換や最適化)
ベクトルの基本操作
加算:ベクトル a と b の和は、対応する成分を足し合わせたものです。
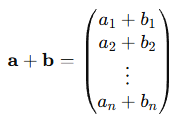
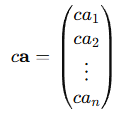
スカラー倍:ベクトルを実数 c 倍する操作
ノルム(大きさ):ベクトルの「長さ」はユークリッド距離で計算されます。
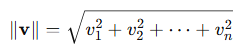
これらの操作は、後に学ぶ勾配降下法や類似度の計算、ニューラルネットワークの重みの調整など、AIのさまざまな場面で登場します。
2.1.2 行列とは何か
行列とは、数値を縦横に並べた「表」のようなもので、数学的には「複数のベクトルをまとめた構造」と考えることができます。
例えば、以下のような2行3列の行列があります:
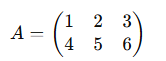
行列は、次のような意味で使われます:
- データの集まりとして:各行が1つのサンプル、各列が特徴量を表す。
- 線形変換として:入力ベクトルを変換し、別の空間へ写す操作。
- システムの記述として:複数の式を一括で表すための記号。
行列の記法と用語
- 行列 A の成分 a₍ᵢⱼ₎ は、i 行 j 列の要素を意味します。
- m × n 行列は、m 行 n 列の行列であることを示します。
- 行ベクトルと列ベクトルは、行列の1行または1列として取り出されるベクトルです。
2.1.3 ベクトルと行列の関係
行列は、複数のベクトルを「並べた」ものとして見ることができます。
たとえば、3つの2次元ベクトルを並べたものは、以下のように行列になります:
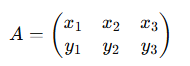
ここで、列ごとに見るとそれぞれが2次元の列ベクトルであり、行列はこれらのベクトルを1つにまとめた構造です。
この見方は、ニューラルネットワークにおけるバッチ処理(複数の入力を同時に処理)を理解するうえで非常に重要です。
2.1.4 AIにおけるベクトルと行列の例
- 画像:モノクロ画像は画素の明暗を表す2次元行列、カラー画像はチャンネルごとの3次元行列。
- テキスト:単語を表すワンホットベクトルや埋め込みベクトル(word2vec、BERTなど)
- ニューラルネットワーク:入力、重み、出力がすべてベクトルや行列であり、演算は行列の積として実行される。
これらの理由から、「AIを理解する」ということは、ベクトルと行列の構造や性質を理解すること」とほぼ同義であると言っても過言ではありません。
演習問題(例)
- 次のベクトル a = (2, -1, 3) のノルム(長さ)を求めなさい。
- 以下の2つのベクトル a = (1, 2)、b = (-3, 4) の和、およびベクトル a のスカラー倍 2a を求めなさい。
- 行列 A = ((1, 2), (3, 4)) の各成分と、その行列の次元を答えなさい。
- 実際の画像データ(例:MNIST)において、1枚の画像を1つのベクトルとして表すにはどうすればよいか、考察せよ。
